
This Time in History In these videos, find out what happened this month (or any month!) in history.#WTFact Videos In #WTFact Britannica shares some of the most bizarre facts we can find.Demystified Videos In Demystified, Britannica has all the answers to your burning questions.Britannica Explains In these videos, Britannica explains a variety of topics and answers frequently asked questions.Britannica Classics Check out these retro videos from Encyclopedia Britannica’s archives.Numerical solutions of these equations show chaotic patterns of this perturbed soliton. Two coupled ordinary differential equations with periodic disturbance are obtained for the soliton amplitude and phase. The adiabatic perturbation result due to Karpman & Maslov (1978) is applied. The third example is the evolution of a single oblique soliton over a periodically varying topography. Whitham's average method is applied to show that the shock wave jump at the wedge vertex develops to a cnoidal wave train and eventually to a solitary wavetrain. The second example deals with the generation of solitary wave-train by a wedge-shaped strut on an even bottom. multi-soliton wave pattern is shown by means of N-soliton solution. This stationary 3-D problem can be reduced from a Boussinesq-type equation into a KdV equation with a forcing term due to uneven topography, in which the transverse coordinate Y plays a same role as the time in original KdV equation. It is considered that a thin strut sits in a supercritical shallow water flow sheet over a homogeneous or very mildly varying topography. The importance of this phenomenon to the study of tsunami action at Hilo, Hawaii, is presented. Results of studies of this phenomenon in the laboratory are presented, together with some observation of its occurrence in the ocean. The Mach-stem is insensitive to undulation, of the wall. Once the Mach-stem is formed, it will continue to grow even when the wall is bent around through almost 90 degrees for periodic waves a Machreflected wave also develops.
The portion of the wave near the wall (called the Mach-stem in air blast waves) increases in height as the wave continues to move along the wall.
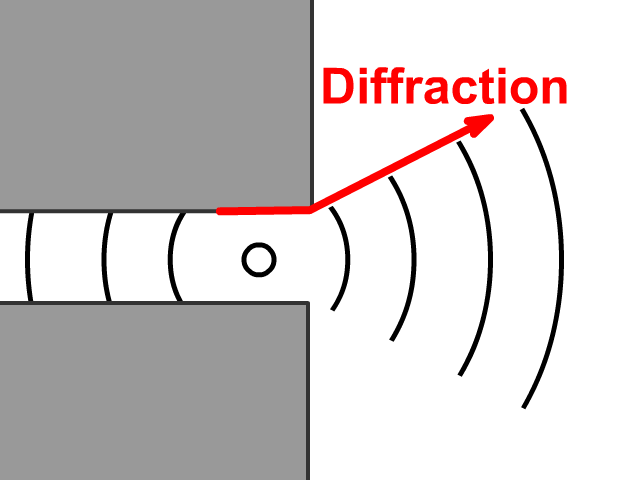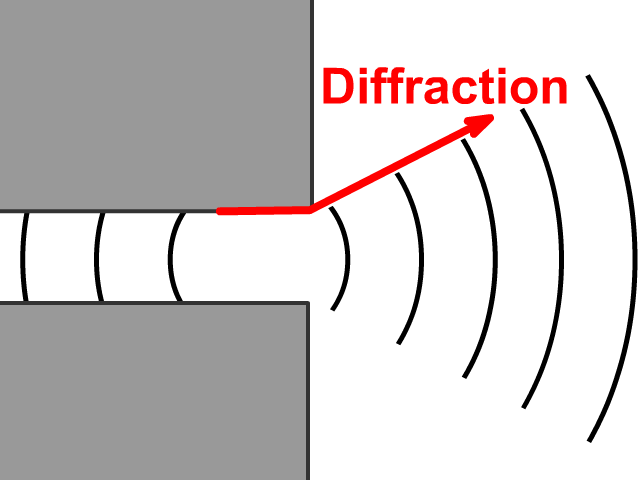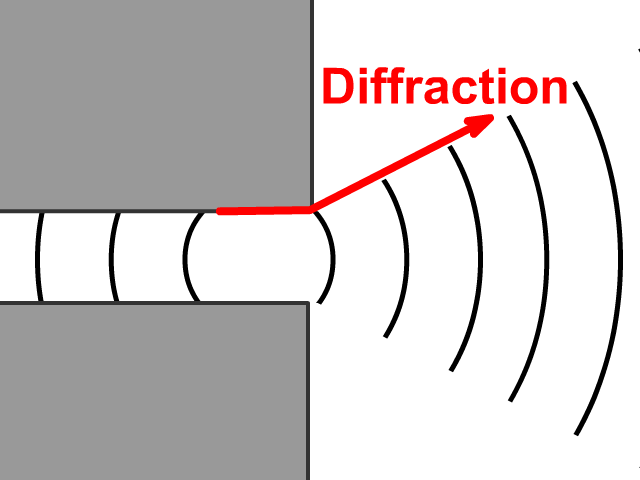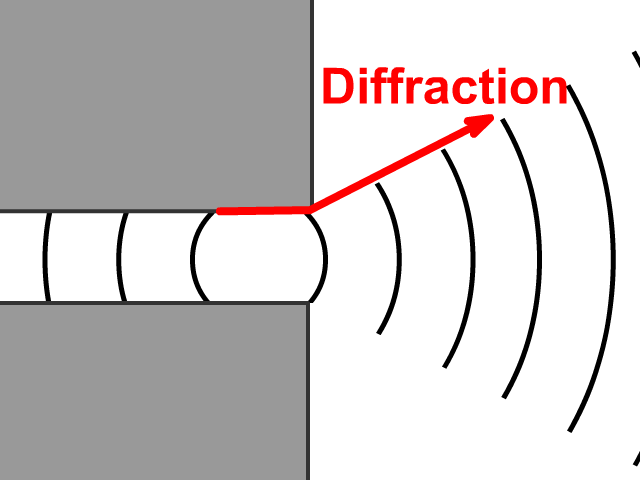
For angles less than about 20 degrees the reflected wave becomes almost negligible. The wave front bends near the wall, becoming normal to the wall, with a small reflected wave. Periodic (shallow water and transitional water) and solitary water gravity waves do not reflect from a wall in the manner commonly supposed, when the angle between the direction of wave advance and the wall is less than about 5? to 45 degrees.
Calculated results are compared with several published shipmodel experiments and other theoretical predictions satisfactory agreement is demonstrated. The numerical procedure for solving the KP equation consists of a finite-difference method, namely, fractional step algorithm with Crank–Nicolson-like schemes in each half step. Besides wave pattern and wave resistance, the hydrodynamic lift force and trim moment are calculated by pressure integration in the fixed-hull case running sinkage and trim, by condition of hydrodynamic equilibrium in the free-hull case.
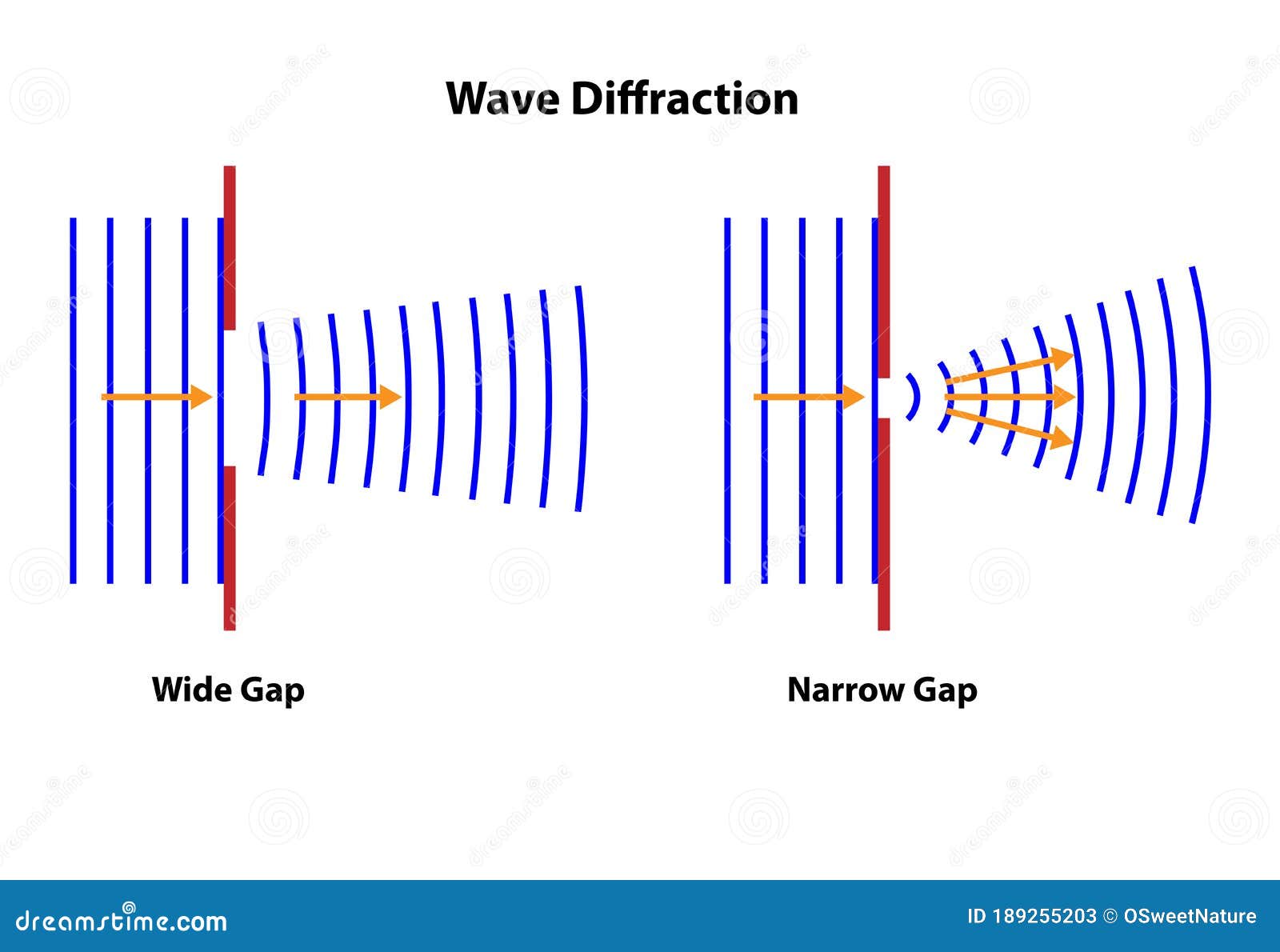
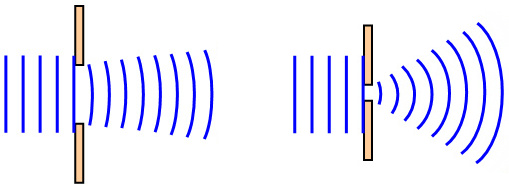
Diffraction of a wave free#
The ship can be either fixed or free to squat. By using the technique of matched asymptotic expansions along with nonlinear shallow-water wave theory, the problem is reduced to a Kadomtsev–Petviashvili equation in the far field, matched with a nearfield solution obtained by an improved slender-body theory, taking the local wave elevation and longitudinal disturbance velocity into account. The problem solved concerns a slender ship moving at a near-critical steady speed in a shallow channel, not necessarily in symmetric configuration, involving the special phenomenon of generation of solitary waves.


 0 kommentar(er)
0 kommentar(er)
